详解js实现线段交点的三种算法

本文讲的内容都很初级, 主要是面向和我一样的初学者, 所以请各位算法帝们轻拍啊
引用

已知线段1（a,b）和线段2（c,d） ,其中a b c d为端点, 求线段交点p .（平行或共线视作不相交）
算法一: 求两条线段所在直线的交点, 再判断交点是否在两条线段上.

求直线交点时我们可通过直线的一般方程 ax+by+c=0 求得（方程中的abc为系数,不是前面提到的端点,另外也可用点斜式方程和斜截式方程,此处暂且不论）.

然后根据交点的与线段端点的位置关系来判断交点是否在线段上.
公式如下图:

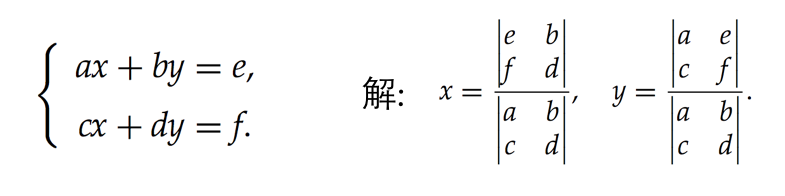
<code class="hljs avrasm">function segmentsIntr（a, b, c, d）{/** 1 解线性方程组, 求线段交点. **/ // 如果分母为0 则平行或共线, 不相交var denominator = （b.y - a.y）*（d.x - c.x） - （a.x - b.x）*（c.y - d.y）;if （denominator==0） {return false;}// 线段所在直线的交点坐标 （x , y）var x = （ （b.x - a.x） * （d.x - c.x） * （c.y - a.y） + （b.y - a.y） * （d.x - c.x） * a.x - （d.y - c.y） * （b.x - a.x） * c.x ） / denominator ;var y = -（ （b.y - a.y） * （d.y - c.y） * （c.x - a.x） + （b.x - a.x） * （d.y - c.y） * a.y - （d.x - c.x） * （b.y - a.y） * c.y ） / denominator;/** 2 判断交点是否在两条线段上 **/if （// 交点在线段1上（x - a.x） * （x - b.x） <= 0 && （y - a.y） * （y - b.y） <= 0// 且交点也在线段2上 && （x - c.x） * （x - d.x） <= 0 && （y - c.y） * （y - d.y） <= 0）{ // 返回交点preturn { x : x, y : y }}//否则不相交return false} </code>

算法一思路比较清晰易懂, 但是性能并不高. 因为它在不确定交点是否有效（在线段上）之前, 就先去计算了交点, 耗费了较多的时间.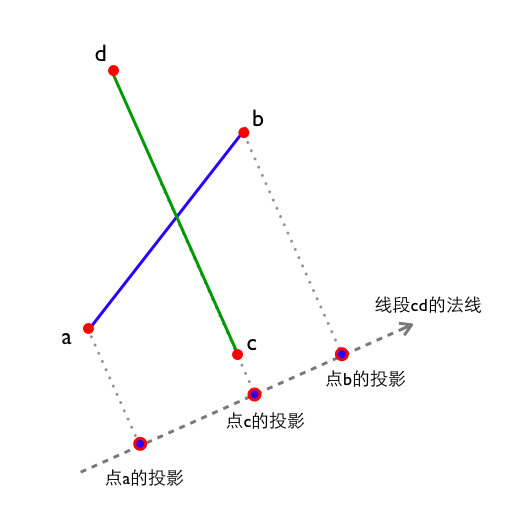

如果最后发现交点无效, 那么之前的计算就白折腾了. 而且整个计算的过程也很复杂.

那么有没有一种思路,可以让我们先判断是否存在有效交点,然后再去计算它呢?

显然答案是肯定的. 于是就有了后面的一些算法.
算法二: 判断每一条线段的两个端点是否都在另一条线段的两侧, 是则求出两条线段所在直线的交点, 否则不相交.

第一步判断两个点是否在某条线段的两侧, 通常可采用投影法:
求出线段的法线向量, 然后把点投影到法线上, 最后根据投影的位置来判断点和线段的关系.
见下图

点a和点b在线段cd法线上的投影如图所示, 这时候我们还要做一次线段cd在自己法线上的投影（选择点c或点d中的一个即可）.

主要用来做参考.

图中点a投影和点b投影在点c投影的两侧, 说明线段ab的端点在线段cd的两侧.
同理, 再判断一次cd是否在线段ab两侧即可.
求法线 , 求投影什么的听起来很复杂的样子, 实际上对于我来说也确实挺复杂,在几个月前我也不会（念书那会儿的几何知识都忘光了 :"（）"

不过好在学习和实现起来还不算复杂, 皆有公式可循
求线段ab的法线:

var nx=b.y - a.y,ny=a.x - b.x; var normalLine = { x: nx, y: ny };

注意: 其中 normalLine.x和normalLine.y的几何意义表示法线的方向, 而不是坐标.
求点c在法线上的投影位置:

var dist= normalLine.x*c.x + normalLine.y*c.y;

注意: 这里的"投影位置"是一个标量, 表示的是到法线原点的距离, 而不是投影点的坐标.

通常知道这个距离就足够了.
当我们把图中点a投影（distA）,点b投影（distB）,点c投影（distC）都求出来之后, 就可以很容易的根据各自的大小判断出相对位置.
       distA==distB==distC 时, 两条线段共线

       distA==distB！=distC 时, 两条线段平行

       distA 和 distB 在distC 同侧时, 两条线段不相交.

       distA 和 distB 在distC 异侧时, 两条线段是否相交需要再判断点c点d与线段ab的关系.

前面的那些步骤, 只是实现了"判断线段是否相交", 当结果为true时, 我们还需要进一步求交点.

求交点的过程后面再说, 先看一下该算法的完整实现 :

function segmentsIntr（a, b, c, d）{ //线段ab的法线N1var nx1 = （b.y - a.y）, ny1 = （a.x - b.x）; //线段cd的法线N2var nx2 = （d.y - c.y）, ny2 = （c.x - d.x）; //两条法线做叉乘, 如果结果为0, 说明线段ab和线段cd平行或共线,不相交var denominator = nx1*ny2 - ny1*nx2;if （denominator==0） {return false;} //在法线N2上的投影var distC_N2=nx2 * c.x + ny2 * c.y;var distA_N2=nx2 * a.x + ny2 * a.y-distC_N2;var distB_N2=nx2 * b.x + ny2 * b.y-distC_N2; // 点a投影和点b投影在点c投影同侧 （对点在线段上的情况,本例当作不相交处理）;if （ distA_N2*distB_N2>=0 ） {return false;} ////判断点c点d 和线段ab的关系, 原理同上////在法线N1上的投影var distA_N1=nx1 * a.x + ny1 * a.y;var distC_N1=nx1 * c.x + ny1 * c.y-distA_N1;var distD_N1=nx1 * d.x + ny1 * d.y-distA_N1;if （ distC_N1*distD_N1>=0 ） {return false;} //计算交点坐标var fraction= distA_N2 / denominator;var dx= fraction * ny1,dy= -fraction * nx1;return { x: a.x + dx , y: a.y + dy }; }

最后求交点坐标的部分所用的方法看起来有点奇怪, 有种摸不着头脑的感觉.

其实它和算法一里面的算法是类似的,只是里面的很多计算项已经被提前计算好了.

换句话说, 算法二里求交点坐标的部分其实也是用的直线的线性方程组来做的.
现在来简单粗略很不科学的对比一下算法一和算法二:

      1、最好情况下, 两种算法的复杂度相同

      2、最坏情况, 算法一和算法二的计算量差不多

      3、但是算法二提供了更多的”提前结束条件”,所以平均情况下,应该算法二更优.
实际测试下来, 实际情况也确实如此.
前面的两种算法基本上是比较常见的可以应付绝大多数情况. 但是事实上还有一种更好的算法.
这也是我最近才新学会的（我现学现卖了,大家不要介意啊…）
算法三: 判断每一条线段的两个端点是否都在另一条线段的两侧, 是则求出两条线段所在直线的交点, 否则不相交.
（咦? 怎么感觉和算法二一样啊? 不要怀疑确实一样 … 囧）

所谓算法三, 其实只是对算法二的一个改良, 改良的地方主要就是 :

不通过法线投影来判断点和线段的位置关系, 而是通过点和线段构成的三角形面积来判断.
先来复习下三角形面积公式: 已知三角形三点a（x,y） b（x,y） c（x,y）, 三角形面积为:

<code class="hljs avrasm">var triArea=（ （a.x - c.x） * （b.y - c.y） - （a.y - c.y） * （b.x - c.x） ） /2 ; </code>

因为两向量叉乘==两向量构成的平行四边形（以两向量为邻边）的面积 , 所以上面的公式也不难理解.

而且由于向量是有方向的, 所以面积也是有方向的, 通常我们以逆时针为正, 顺时针为负数.
改良算法关键点就是:

如果”线段ab和点c构成的三角形面积”与”线段ab和点d构成的三角形面积” 构成的三角形面积的正负符号相异,

那么点c和点d位于线段ab两侧.
如下图所示:

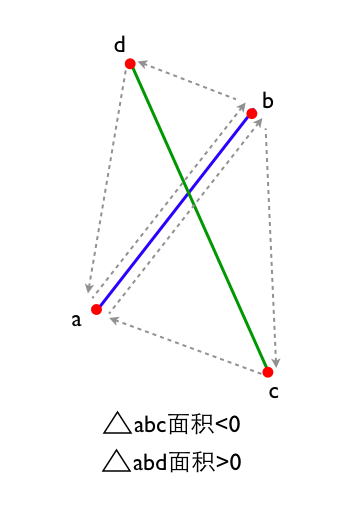
图中虚线所示的三角形, 缠绕方向（三边的定义顺序）不同, 所以面积的正负符号不同.
下面还是先看代码:

由于我们只要判断符号即可, 所以前面的三角形面积公式我们就不需要后面的除以2 了.

function segmentsIntr（a, b, c, d）{ // 三角形abc 面积的2倍var area_abc = （a.x - c.x） * （b.y - c.y） - （a.y - c.y） * （b.x - c.x）; // 三角形abd 面积的2倍var area_abd = （a.x - d.x） * （b.y - d.y） - （a.y - d.y） * （b.x - d.x）; // 面积符号相同则两点在线段同侧,不相交 （对点在线段上的情况,本例当作不相交处理）;if （ area_abc*area_abd>=0 ） {return false;} // 三角形cda 面积的2倍var area_cda = （c.x - a.x） * （d.y - a.y） - （c.y - a.y） * （d.x - a.x）;// 三角形cdb 面积的2倍// 注意: 这里有一个小优化.不需要再用公式计算面积,而是通过已知的三个面积加减得出.var area_cdb = area_cda + area_abc - area_abd ;if （ area_cda * area_cdb >= 0 ） {return false;} //计算交点坐标var t = area_cda / （ area_abd- area_abc ）;var dx= t*（b.x - a.x）,dy= t*（b.y - a.y）;return { x: a.x + dx , y: a.y + dy };}

最后计算交点坐标的部分和算法二同理.
算法三在算法二的基础上, 大大简化了计算步骤, 代码也更精简. 可以说,是三种算法里, 最好的.实际测试结果也是如此.
当然必须坦诚的来说, 在Javascript里, 对于普通的计算, 三种算法的时间复杂度其实是差不多的（尤其是V8引擎下）.
我的测试用例里也是进行变态的百万次级别的线段相交测试才能拉开三种算法之间的差距.
总结
不过本着精益求精以及学习的态度而言, 追求一个更好的算法, 总是有其积极意义的。以上就是利用js实现线段交点的几种算法，内容不是很深奥，希望对大家学习js有所帮助。